Geometric-k-means

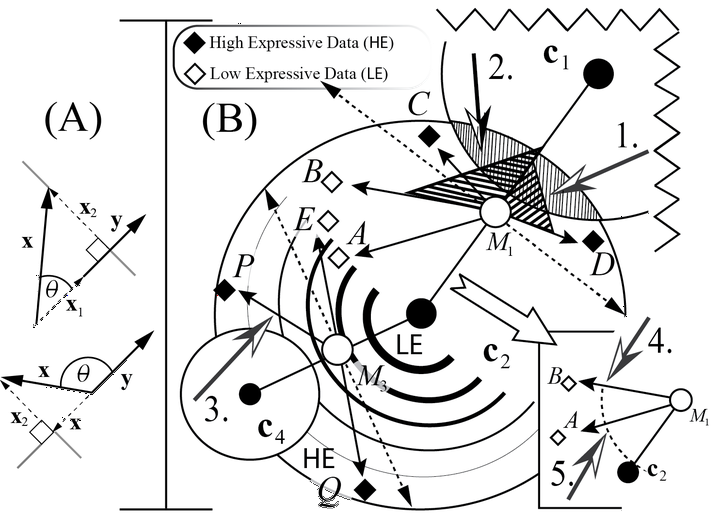
K-means is among the most widely used ML algorithms, even though it is more than 50 years old. Recent optimizations focus on reducing distance calculations (DC). Two approaches dominate: bounded and unbounded. Bounded DC place a priori bounds on the number of reductions, while unbounded does not. Unbounded exists as a popular improvement called Ball-k-means that determines what data can be safely ignored for a subsequent iteration. In this work, we describe a novel second unbounded DC reduction by leveraging geometry: specially, scalar projection, that helps reduce more DC. This approach is linear w.r.t. to the centroid’s members, unlike Ball-k-means, which requires sorting. Experiments on real-world and synthetic data demonstrate that geometric approach, which we call Geometric-k-means (or Geo-k-means for short), is significantly better. Additionally, replacing multiple instances of k-means in a state-of-the-art (SOTA) pipeline for high dimensional computational biology data with Geo-k-means and Ball-k-means demonstrates that this approach is superior in a real-world application. Geo-k-means relies on the notion of data expressiveness, where high expressive data significantly affects the objective function, while low expressive does not. By separating high/low expressive data in each iteration, we effectively ignore a significant number of DC which results in substantially reduced run-time while preserving the accuracy.