Telescope Indexing for k-Nearest Neighbor Search Algorithms

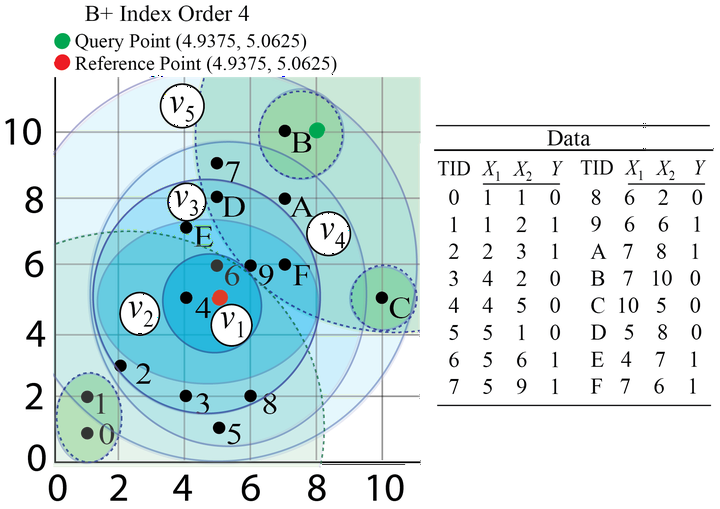
When k-Nearest-Neighbors (k-NN) was conceived more than 70 years ago, computation, as we use it now, would be hardly recognizable. Since then, technology has improved by orders of magnitude, including unprecedented connectivity. However, k-NN has remained virtually unchanged, exposing its shortcomings for today’s needs: becoming overwhelmed when presented with large, high-dimensional data. Although space partitioning data structures, especially k-d trees and ball-trees, have improved performance in larger data, they remain inadequate when data is also high-dimensional. Experiments confirm that space partitioning becomes ineffective in high-dimensional data because most of the search space is explored needlessly. Our strategy is to partition the data into small groups of points similarly distanced from a reference point in B+ tree data structure and use this data structure to limit the search space of a k-NN query. Further, we establish that the limited search space chosen by the B+ tree structure can be effectively explored by any indexing techniques applicable to the entire data. We then present our algorithm k-NN with partitioning (tik-NN), including computational analysis and experiments. Our detailed evaluation demonstrates significant speedup achieved by tik-NN over the naive, k-d tree, ball-tree based k-NN and other the state-of-the-art approximate k-NN search approaches in high dimensional data.